A quick (maybe) update on things. I've gotten the C version of the code in line with the Python/Pygame version, but I need to organize the code a little better.
I found myself solving a problem that many have solved before: How do you know if the mouse is within a diamond shape?
The answer comes from the pre-algebra maths: "Calculating the slope of a line" -> y = mx + b
The tricky part is that you're calculating x based on what's happening in y, and vice versa.
These are the basic lines we're after:
y = x/2 + b
x = -2y + b
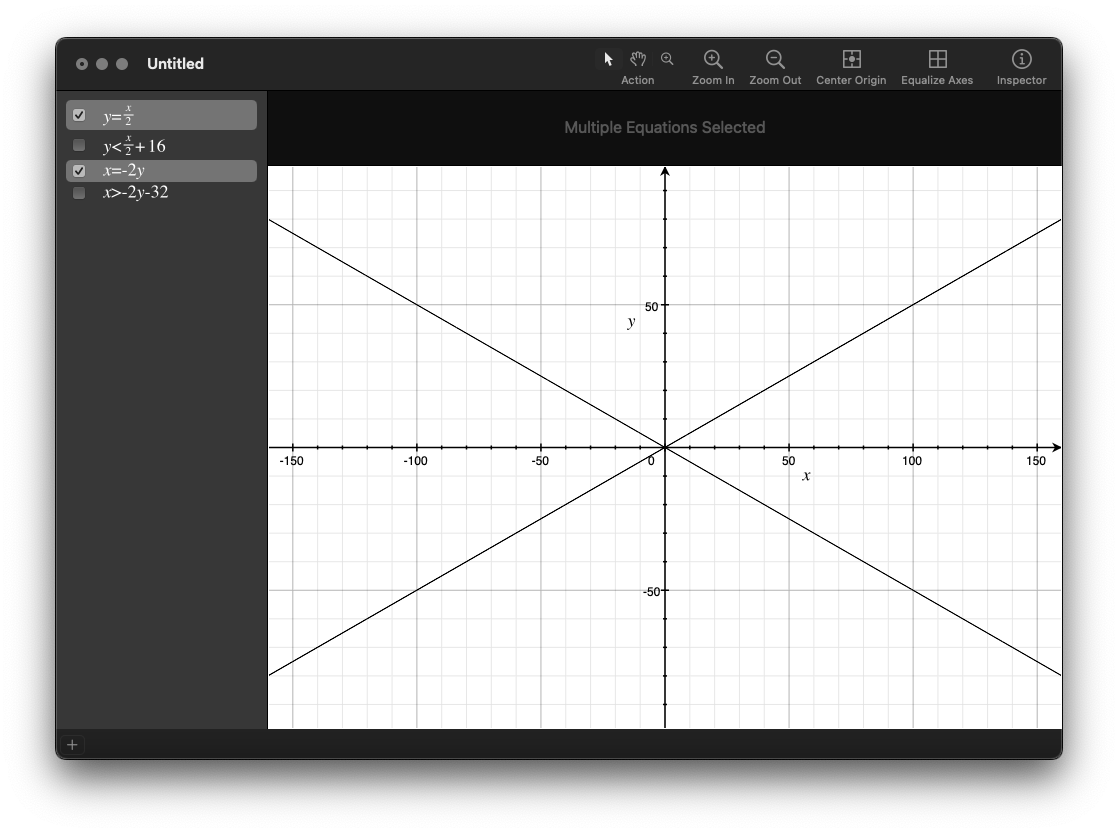
For this exercise I'm checking a diamond shape that's 64 pixels wide and 32 pixels tall, so we're looking for what's in the middle of this shape:
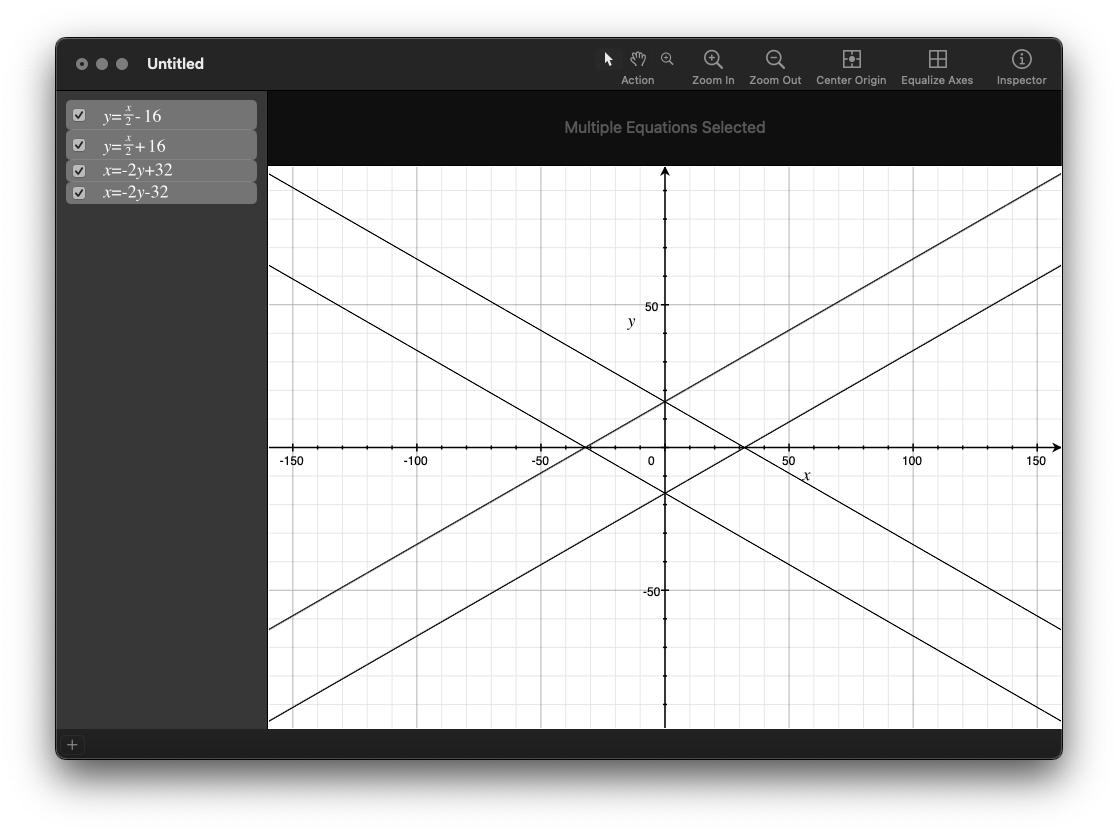
If you have point (0, 0), and your mouse is around (5, 5), we'll call those variables (x, y) and (mouse_x, mouse_y). For this scenario at the origin, we can say:
mouse_x < -2 * y + 32
mouse_x > -2 * y - 32
mouse_y > x / 2 - 16
mouse_y < x / 2 + 16
This is what it looks like in OSX's Grapher app:
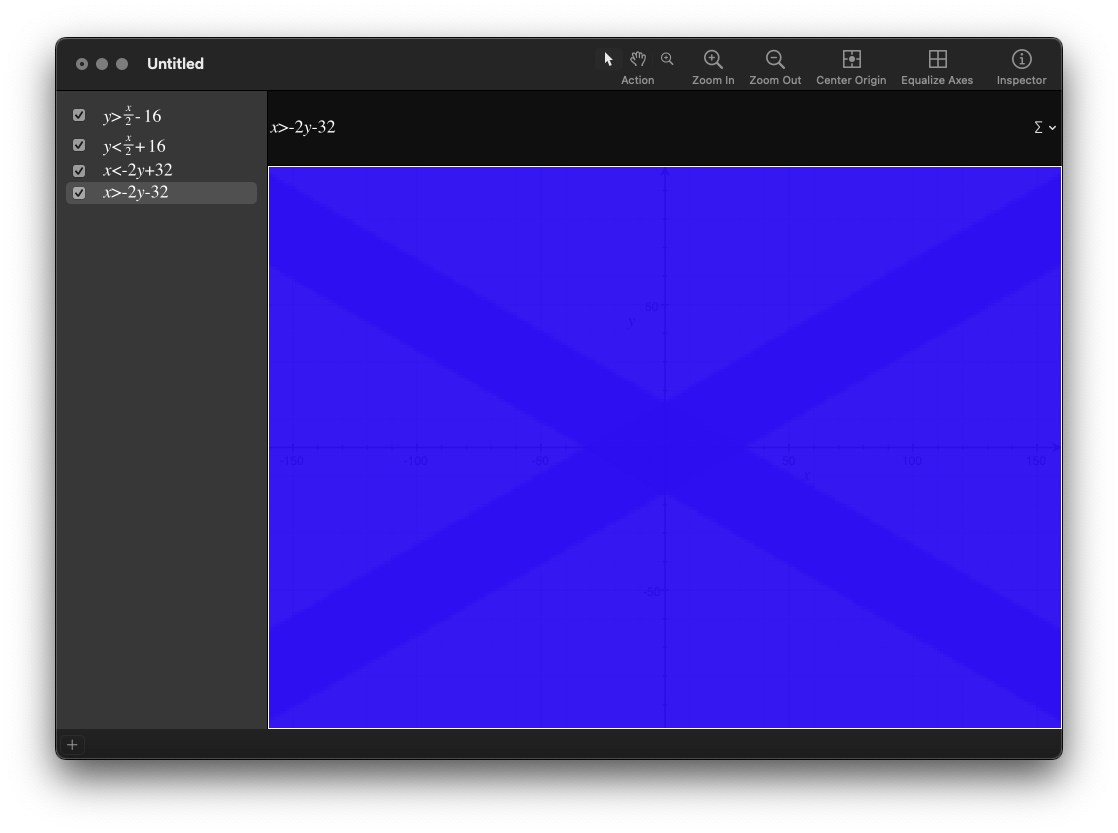
That formula works great if you're at the origin, but once you move away from that you need to compensate a little:
mouse_x - x < -2 * (mouse_y - y) + 32
mouse_x - x > -2 * (mouse_y - y) - 32
mouse_y - y > (mouse_x - x) / 2 - 16
mouse_y - y < (mouse_x - x) / 2 + 16
and since we're adding the same stuff twice for each formula, let's do that ahead of time:
dx = mouse_x - x
dy = mouse_y - y
dx < -2 * dy + 32
dx > -2 * dy - 32
dy < dx / 2 - 16
dy < dx / 2 + 16
Now: you could simplify even more by getting the absolute value of dx and dy up front:
dx = abs(mouse_x - x)
dy = abs(mouse_y - y)
dx < -2 * dy + 32
dy < dx / 2 - 16
And here's the result: A yellow oval moving from cell to cell in the isometric map: